A. Tóm tắt lý thuyết

Để khảo sát sự biến thiên của hàm số, tức tìm các khoảng hàm số đồng biến hoặc nghịch biến (còn gọi là tính đơn điệu của hàm số), ta có thể tiến hành như sau :

- Tìm tập xác định D (khoảng, đoạn hay nửa khoảng) của hàm số f.

- Nếu hàm f liên tục và có đạo hàm trên D ta tính đạo hàm và xét dấu đạo hàm để áp dụng :

+ Hàm f đồng biến (hay tăng) trên D ⇔ f’(x) > 0, 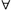x ∈ D.

+ Hàm f nghịch biến (hay giảm) trên D ⇔ f’(x) ≤ 0, 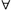x ∈ D. (Dấu = chỉ xảy ra tại những điểm rời rạc).

+ Hàm f không đổi trên D ⇔ f’(x) = 0, 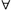x ∈ D.

Ta lập bảng biến thiên thể hiện sự xét dấu f'(x) đế biểu diễn tính đơn điệu của hàm số.

Ghi chú:
. Hàm số đồng biến trên D có đồ thị đi lên từ trái sang phải.
. Hàm số nghịch biến trên D có đồ thị đi xuống từ trái sang phải.
. Hàm số không đổi trên D có đồ thị là đường thẳng vuông góc với trục tung.

B. Ví dụ:

Xét sự biến thiên của hàm số: 

                                                   Giải

Hàm số có tập xác định D = R

y' = x² - 5x + 4

Bảng biến thiên

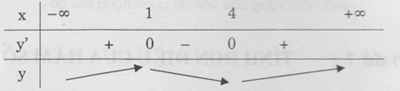
Vậy hàm số tăng trên hai khoảng (-∞ ; 1), (4 ; +∞) và giảm trên khoảng (1 ; 4)

Áp dụng: Tính đơn điệu của hàm số có thể được áp dụng để chứng minh một số bất đẳng thức

Ví dụ: Chứng minh sinx < x với mọi x > 0

                                              Giải

Đặt f(x) = sinx - x. Ta có f(x) là hàm số liên tục trên R.

Đạo hàm f'(x) = cosx - 1 < 0, với mọi x thuộc R.

Vậy hàm số f(x) nghịch biến trên R nên với x > 0 suy ra f(x) < f(0) hay sinx - x < 0 với mọi x > 0

Do đó sinx < x với mọi x > 0.