Thể tích của khối đa diện
1. Thể tích hình hộp, hình lăng trụ
• Thể tích hình hộp chữ nhật bằng tích ba kích thước.
V = abc
• Thể tích hình lăng trụ bằng tích số của diện tích đáy và chiều cao.
V = Sđáy.h
Chiều cao của lăng trụ là khoảng cách giữa hai mặt đáy.
2. Thể tích hình chóp
Thể tích hình chóp bằng một phần ba tích của chiều cao và diện tích đáy.
V =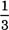 
Sđáy.h
3. Một số tính chất cần nhớ
• Tỉ số thể tích của hai hình tứ diện: Nếu A', B’, C' là các điểm tùy ý trên các cạnh của tứ diện S.ABC thì
• Một phép vị tự tỉ số k biến khối đa diện có thể tích V thành khối đa diện có thể tích V’ thì :
• Để tính thể tích rnột khối đa diện phức tạp, người ta thường phân chia khối đa diện đó thành các khối đa diện như hình chóp, hình lăng trụ. Khi dó, thể tích khối đa diện cần tính là tống thể tích các khối đa diện thành phần. Trong một số trường hợp, thể tích khối đa diện cần tính được xem là hiệu của hai khối đa diện.
• Hình lăng trụ ABC.A’B’C’ được chia thành ba tứ diện có thể tích bằng nhau bởi các mặt phẳng (A'BC) và (A’B’C).
Chú ý: Khi làm các câu hỏi thuộc dạng trắc nghiệm, học sinh sử dụng các tính chất đã biết của các khối đa diện thường gặp mà không phải lập lại chứng minh vì thời gian không đủ cho các chứng minh tính chất. Những tính chất thường dùng của hình hộp, hình hộp chữ nhật, hình chóp đều, hình chóp cụt đều, ... là những tính chất thường dùng. Các lời giải trong các bài ở phần bài tập cũng được trình bày theo quan điểm đó.
