Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
A. TÓM TẮT LÝ THUYẾT
1. Định nghĩa:
♦ Để chứng minh M là giá trị lớn nhất của hàm số f trên tập xác định D, ta cần chứng tỏ :
a) f(x) ≤ M,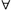 
x ∈ D ;
b) ∃x0 ∈ D để f(x0) = M.
♦ Để chứng minh m là giá trị nhỏ nhất của hàm số f trên tập xác định D, ta cần chứng tỏ :
a) f(x) ≥ m, 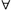x ∈ D ;
b) ∃x0 ∈ D để f(x0) = m.
2. Phương pháp tổng quát
để xác định giá trị lớn nhất và giá trị nhỏ nhất của hàm số f trên tập xác định D
là lập bảng biến thiên của hàm số f với đầy đủ các giá trị đặc biệt của y, từ đó ta sẽ suy ra được:
| max f(x) ; | min f(x). |
| D | D |
Ghi chú:
1. f(x) là biểu thức lượng giác.
- Ta biến đổi để trong biểu thức chỉ còn chứa y = sin(ax + b) hay y = cos(ax + b)
và áp dụng : -1 ≤ sin( ax + b)≤ 1, 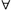x ∈ R
-1 ≤ cos( ax + b)≤ 1, 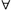x ∈ R
Trường hợp f(x) chứa sin(ax + b), cos(ax + b) và ta biến đổi được về dạng: Asin(ax + b) + Bcos(ax + b) = C thì áp dụng điều kiện phương trình có nghiệm : A2 + B2 ≥ C2.
2. Trường hợp y = f(x) liên tục trên đoạn [a ; b], ta tiến hành các bước:
- Tìm các giá trị của x sao cho f'(x) = 0 hay f'(x) không xác định trên đoạn [a ; b], giả sử các giá trị đó là x1, x2, x3.....
- Tính các giá trị của hàm số tại các điểm có giá trị x nói trên là f(x1), f(x2), f(x3),.........
- Tính giá trị của hàm số tại hai đầu mút là f(a), f(b).
- So sánh các giá trị f(a), f(b), f(x1), f(x2), f(x3), ta suy ra giá trị nhỏ nhất và lớn nhất của f(x) trên đoạn
[a ; b]
3. Nếu trong miền D có f(x) → +∞ thì hàm số không có giá trị lớn nhất trong D. Nếu trong miền D có f(x) → -∞ thì hàm số khônq có giá trị nhỏ nhất trong D.
4. Nếu hàm số f liên tục và đạt cực trị duy nhất trong khoảng (a ; b) tại x0 thì:
| max f(x) = f(x0) nếu cực trị trên là cực đại ; (a ; b) |
| min f(x) = f(x0) nếu cực trị trên là cực tiểu. (a ; b) |
Ví dụ 1. Giá trị lớn nhất và nhỏ nhất của hàm số y = x3 - 3x2 - 9x + 1 trên đoạn [- 2 ; 4] lần lượt là
(A) -1 ; -19 ; (B) 6 ; -26 ;
(C) 4 ; -19 ; (D)10;-26.
Giải
Hàm số liên tục trên đoạn [-2 ; 4] và có đạo hàm y’ = 3x2 - 6x - 9.
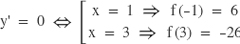
Giá trị của hàm số tại hai đầu mút: f(-2) = -1 ; f(4) = -19
So sánh các giá trị vừa tính được của hàm số, ta suy ra
| max f(x) = 6; [-2 ; 4] |
min f(x) = -26 [-2 ; 4] |
Chọn phương án (B)
