1. Phương trình, hệ phương trình mũ và lôgarit

* Với phương trình mũ và lôgarit, phương pháp giải tổng quát là dựa vào định nghĩa:

         a^x = m ⇔ x = log_am (là nghiệm duy nhất).

Với m < 0 thì phương trình trên vô nghiệm.

         log_ax = m ⇔ x = a^m (là nghiệm duy nhất ∀m ∈ R),

2.  Ngoài ra, ta có một số cách giải đặc biệt:

- Biến đổi các cơ số trong phương trình mũ hoặc lôgarit về cùng một cơ số để đưa về dạng áp dụng được tính chất:

       a^f(x) = a^g(x) ⇔  f(x) = g(x)
       log_af(x) = log_ag(x) ⇔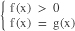  

- Biến đổi để trong phương trình chỉ còn một loại hàm mũ hoặc lôgarit duy nhất để có thể đặt nó làm ẩn

phụ và đưa phương trình về dạng mới theo ẩn phụ.

3. Một số phương trình mũ có cơ số khác nhau mà không biến đổi để đưa được về cùng một cơ số, ta có

thể thu gọn để có điều kiện lôgarit hoá hai vế theo cùng một cơ số thích hợp nhằm làm gọn lời giải.

4. Một số phương trình mũ hoặc lôgarit ở dạng không mẫu mực, tức cách giải tuỳ thuộc đặc thù của từng

phương trình, thông thường là có thể tính nhẩm trước một nghiệm của phương trình và chứng tỏ nghiệm

này là duy nhât dựa vào tính đơn điệu của hàm số hoặc dựa vào phương pháp đối lập:

* Với hệ phương trình mũ và lôgarit ta kết hợp cách giải hệ phương trình đại số với cách giải phương trình

mũ và lôgarit.
Ví dụ: Nghiệm của phương trình 3^{2 + x} + 3^{2 - x} = 30 là kết quả nào sau đây ?

A.  x = 0             B. x = 3            C. x = ±1            D. Phương trình vô nghiệm.

                                                 Giải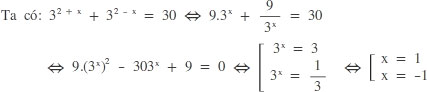

Chọn C.